Seat Exchange: A Coincidence of Wants or Simultaneous Game?

Can we design an economic model of passenger-to-passenger seat exchanges directly between passengers?

If such a model exists, we wish to further consider a passenger audience meeting the following constraints for the air travel use case:

• ticketed passengers of a commercial flight with publicly available information,
• passengers possessing a mobile device with GPS and a machine-readable seat assignment,
• passengers physically present in the waiting area prior to boarding the aircraft, and
• passengers willing to consider multiple offers before choosing or declining seat offers.

Why place those restrictions on the qualification of passengers? We can take them one at a time to explain further.

Simplified Economically Coincident Model

The above constraints satisfy and meet the criteria for a "double coincidence of wants", from microeconomics. An economic model needs a buyer and seller. We expect goods or services exchanged in this use case to be an exchange of assigned seats between passengers.

The exchange transaction costs rely on a means of exchange as a mobile device to transmit the information. We rely also on a quantifiable means of valuation and assessment as presumably a fiat currency, like money, or a points-based conversion equivalent, or an incentivized discounted rate such as convertible coupons and tokens for other goods and services.

This model then assumes an economic market with a lower barrier to facilitate coincident exchange of wants and needs by automatically determining the buyer and seller. The automation thereby ensures adherence to the assumptions of this microeconomic model:

• Same time and place,
• Coincident wants,
• Coincident needs,
• Coincident time and place (i.e. a flight event),
• In-kind or "like for kind" transfer as an atomic transaction (i.e. "all or none"), and
• A voluntary and agreed upon medium of exchange (i.e. a seat on the flight).

We presuppose here that the medium of exchange includes the agreeable exchange of one person occupying one seat. We also assume that in addition to money to incentivize and rebalance perceived valuation that we automatically determine, or deduce, a quantitive difference in seat valuation based on a qualitative differential in valuation. Meaning, what I qualitatively value highly you may discount as a low quality, or vice versa.

This economic analysis of curves can include a Quantity-Price graph, illustrated in Figure 1, below, which shows seat demand curves, D₀1 and D₀2, and seat supply curve, S (as seats on the same flight), rising as possibly modeled by a power law, such as Pareto, or a quadratic, with demand curve D expressed as an inverse power law (red lines).

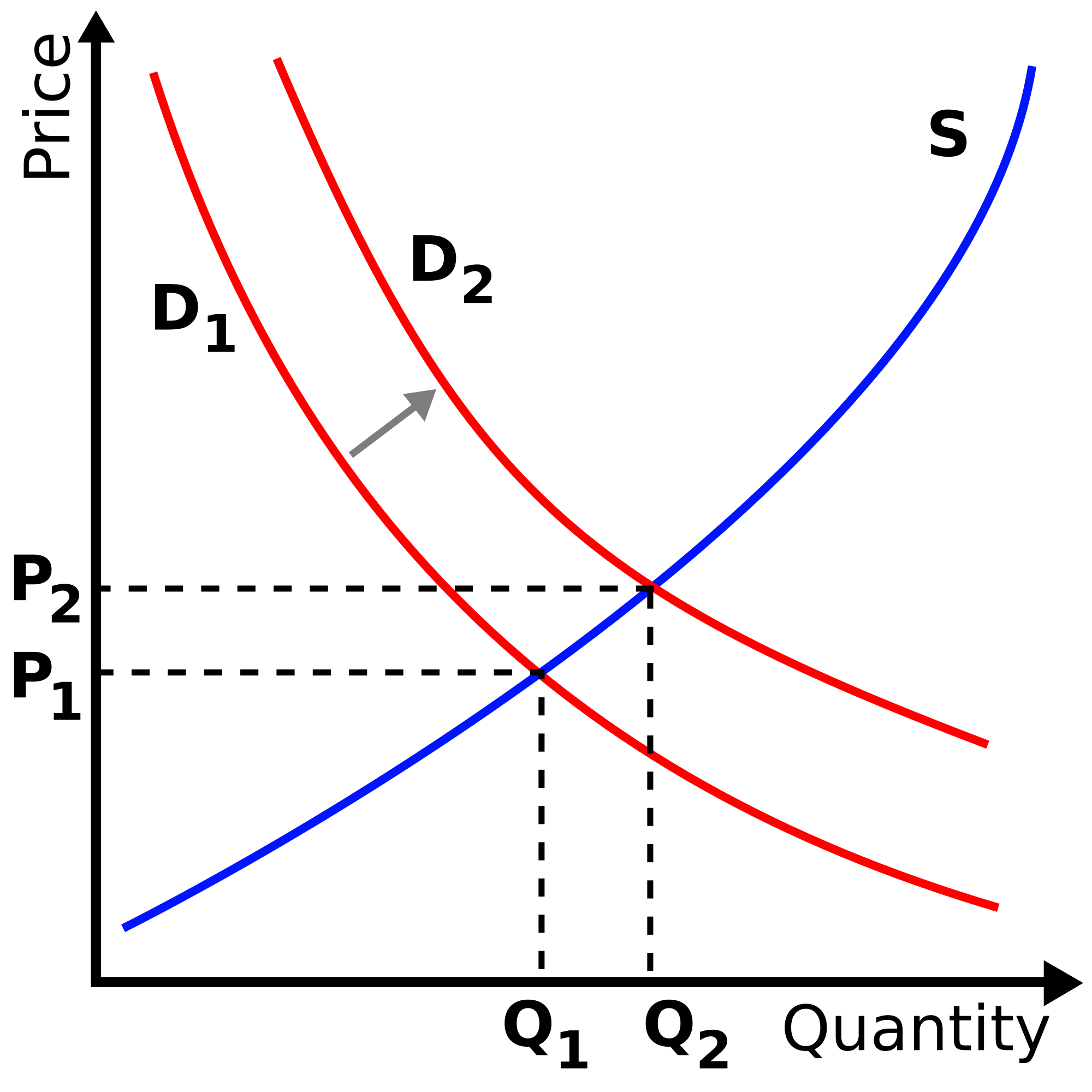Figure 1: Courtesy of Wikipedia.org, supply and demand diagram illustrates increase in demand.

Direct Seat Match

We expect matches occurring in Quadrant I to be a direct match per the description in blog post, "Direct Match Cooperation". Figure 2 is reproduced from a previous blog post graphic. It illustrates the four seat exchange quadrants. We will refer to the quadrants as numbered 1 through 4, in clockwise fashion, starting from the upper left-hand corner. The "Reciprocal Seat Match Quadrants" shows a simplified model with only two passengers considering a voluntary seat exchange directly with one another on the same flight.

Quadrant 3, the lower-left use case, may possibly be disregarded by both passengers. Although it does define very useful automation system meta-data. The Quadrant 3 region represents a use case where neither party matches with the other passenger's seat because each passenger possesses a seat of direct opposition to the other passenger's desired seat prototype.

Figure 2: Seat Match Quadrants for 2 Passengers

Quadrant 2, in the upper right-hand region, is the search region of a reciprocal direct match. Passenger matches identified from the set of all potential passenger-to-passenger matches warrant further inspection for likelihood of exchange. SeatBot can open a path to negotiation between these passenger to passenger cooperative exchanges. A likelihood prediction based on historical activity generates added value to a match prediction as a filter.

A prediction filter gets applied prior to notifying either passenger. We use this to improve match confidence intervals illustrated by the multi-layered flame-shaped diagram annotated with smiley faces in the "Fitness of Seat X for Passenger Y" diagram on the left hand side above. These regions are shaded green to represent their contour on the Z-axis, which is not shown in the 2D diagram.

Negotiated Wants by Exchange Quadrants

The question remained as to how to model all possible passenger to passenger exchanges of seats instead of only a portion. The negotiation quadrants are the top-left and lower-right (quadrants 1 and 4) where a spread exists between passenger valuations. These quadrants match one passenger with an upside gain against another with a downside loss.

The economic models neglect to give either passenger any guidance or advice from the automation. The system has information that could be used to:

1. provide recommendations of likelihood as guidance,
2. match buyers to a seller to create markets, 
3. match sellers to a buyer to stimulate commerce,
4. answer questions for helpful information,
5. satisfy seat preference for resource matching to need,
6. maintain impartiality to control bias.

If this information were codified, then a model of behavior might emerge. A probability based algorithm could select seat suggestions from available passengers and let the passengers decide, thereby providing feedback. The probabilistic model could make adjustments and proceed to another suggestion round.

This had us asking, "What if we modeled portions of the passenger audience as a Simultaneous Game?" And so, how would that work? We decided that seats are arranged a specific pattern, in a two-dimensional grid. Seat maps are ordered as rows and each row has a group of seats attached to a single seat frame bolted to the aircraft floor. Seats are further characterized into columns spanning across the aircraft body from window to an aisle, followed by zero, one or more aisles, finally terminating again in an aisle to window grouping. It appears very similar to a game board with pieces moving linearly in two dimensions; hence the company name as Hopscotch Solutions.

If this were a Simultaneous Game, who moves against whom? Are there strategies to employ? Is there always a "winner" and a "loser"? And does it happen at the same time without a priori knowledge of the other player move?

If passenger preference were exchanged confidentially with a third party, and that information were used to confer and reliably assign a computed numerical valuation, then yes, we might say the seat preference of each and every passenger matters. The third party would need to be told confidentially who wants what from a seat location. Also, we would run the offers across multiple timed game rounds. And the game would have to eventually end prior to boarding, possibly producing zero, two, or more even numbers of passenger-to-passenger reseating exchanges.

Now, if the automation were considered a third party holding preference information, then preference to seats can be matched on goodness of fit modeled as a vector. Okay, then what if we model seat and preferences as vectors? What does a goodness of fit against for a set of passengers look like?